什么是无穷小量等价代换的公式,以及如何应用它?
在探讨数学领域的深邃奥秘时,一个至关重要的概念便是“无穷小量等价代换”。这一技巧不仅简化了复杂的极限计算,还为求解微分方程、进行泰勒展开以及研究函数渐近线等问题提供了强有力的工具。本文将深入解析无穷小量等价代换的公式及其应用,旨在吸引那些对此充满好奇与探索欲的读者。
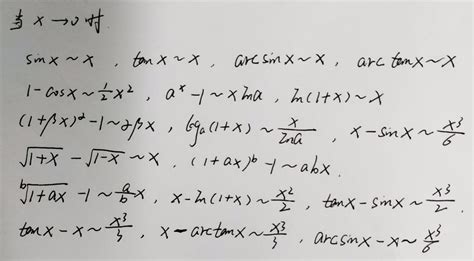
无穷小量等价代换的定义
首先,让我们明确什么是无穷小量。当自变量x趋近于某个特定值(如0或无穷大)时,如果函数f(x)的极限为0,则称f(x)为该点附近的无穷小量。特别地,若两个无穷小量f(x)和g(x)在x趋近于某一点时,它们的比值的极限为1,即$\lim_{{x \to x_0}} \frac{f(x)}{g(x)} = 1$,则称f(x)和g(x)在该点附近是等价无穷小,记作$f(x) \sim g(x)$(当$x \to x_0$)。
等价无穷小代换的公式
在x趋近于0的情况下,一系列常见的等价无穷小代换公式包括但不限于:
1. 三角函数类:
$\sin x \sim x$
$\tan x \sim x$
$\arcsin x \sim x$
$\arctan x \sim x$
$1 - \cos x \sim \frac{x^2}{2}$
这些公式揭示了三角函数在极限情况下的简化形式,使得复杂的三角函数表达式得以简化为更易处理的线性表达式。
2. 指数与对数类:
$e^x - 1 \sim x$
$\ln(1+x) \sim x$
$a^x - 1 \sim x \ln a$(其中a为常数)
这些公式揭示了指数函数和对数函数在自变量趋于0时的行为特征,对于处理涉及这些函数的极限问题极为有用。
3. 幂函数与多项式类:
当n为正整数时,$(1+x)^n - 1 \sim nx$
$\sqrt[n]{1+x} - 1 \sim \frac{x}{n}$
这些公式在处理幂函数和多项式的极限问题时,能够显著简化计算过程。
应用场景与注意事项
等价无穷小代换在求解极限问题中尤为常见,它能够化繁为简,将复杂的函数表达式转化为更易处理的形式。然而,在应用过程中也需注意以下几点:
1. 适用条件:等价无穷小代换仅适用于乘积或除法中的因子替换,对于和差项则不能直接替换,因为可能会忽略掉不能忽略的高阶项。
2. 精度控制:在进行等价无穷小代换时,需要确保替换后的表达式与原始表达式在所需精度范围内是一致的。否则,可能会引入额外的误差。
3. 适用范围:虽然等价无穷小代换在x趋近于0时最为常用,但在某些情况下,它也可以推广到x趋近于其他值或无穷大的情况。然而,这需要具体问题具体分析,不能一概而论。
示例解析
为了更直观地展示等价无穷小代换的应用,我们来看一个具体的例子:
求极限$\lim_{{x \to 0}} \frac{\tan x - \sin x}{x^3}$。
若直接进行替换,可能会得到错误的答案(如文章开头提到的错解)。正确的做法是利用三角函数的泰勒展开式:
$$\tan x = x + \frac{x^3}{3} + o(x^3)$$
$$\sin x = x - \frac{x^3}{6} + o(x^3)$$
代入原式得:
$$\lim_{{x \to 0}} \frac{\left(x + \frac{x^3}{3} + o(x^3)\right) - \left(x - \frac{x^3}{6} + o(x^3)\right)}{x^3} = \lim_{{x \to 0}} \frac{\frac{x^3}{2} + o(x^3)}{x^3} = \frac{1}{2}$$
通过这个例子可以看出,等价无穷小代换需要结合泰勒展开式等高级工具来确保计算的准确性。
结语
无穷小量等价代换是数学分析中的一项重要技巧,它不仅简化了复杂的极限计算过程,还拓展了数学方法的应用范围。通过深入理解和掌握这一技巧及其背后的原理和应用场景,我们能够更好地
- 上一篇: 如何取消支付宝的免密支付设置?
- 下一篇: XL号裤子对应的具体尺码是多少?
新锐游戏抢先玩
游戏攻略帮助你
更多+-
02/08
-
02/08
-
02/08
-
02/08
-
02/08









