揭秘几何殿堂的钥匙：正弦定理与余弦定理的深度解析

在数学的浩瀚星空中，有两颗璀璨的星辰，它们照亮了我们在解决三角形相关问题时的道路，这便是正弦定理与余弦定理。想象一下，你正站在一个风景如画的三角形地带，手中拿着测量工具，想要知道这三点之间的距离关系或是某个角的度数，正弦定理和余弦定理就像是你的超级导航，指引你轻松找到答案。接下来，让我们以一种轻松而深入的方式，探索这两大定理的奥秘。

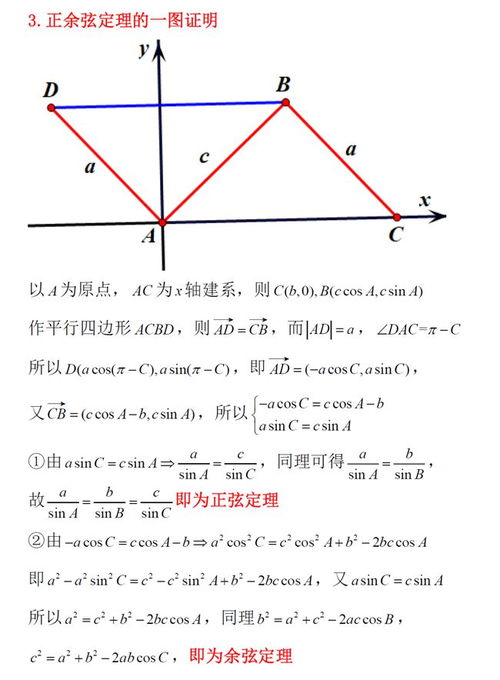
正弦定理：三角形的“和谐之音”

首先登场的是正弦定理，它仿佛是三角形内部的一个美妙和弦，揭示了三角形边长与其对应角正弦值之间的和谐关系。想象一下，你站在一个三角形ABC的任意一个顶点，比如A点，望着对面的边BC，心中充满了对BC长度的好奇。正弦定理告诉你，不需要直接测量，只要知道BC所对的角A的大小，以及另外两个角B和C对应的两边AB和AC的长度，你就能通过一种“魔法”公式计算出BC的长度。

这个“魔法”公式就是正弦定理的表达式：

\[ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} \]

其中，a、b、c分别是三角形ABC的三边长，A、B、C分别是它们对应的角。正弦定理告诉我们，在任何三角形中，任意一边的长度与其对应角的正弦值的比值都是相等的，这是一个非常强大的性质，使得我们可以在知道其中两个元素时，轻松求解第三个元素。

应用场景：正弦定理在航海、天文学、地图制作等领域都有广泛应用。比如，在航海中，利用已知的两点间距离和观测到的角度，可以计算出船只与某个地标之间的直线距离，这就是正弦定理大显身手的时候。

余弦定理：三角形的“稳固支柱”

接下来，让我们把目光投向余弦定理，它是三角形的另一根坚实支柱，尤其在处理三角形边长与角度的直接关系时，显得尤为重要。如果说正弦定理让我们能够通过角度来推算边长，那么余弦定理则允许我们直接通过边长的信息来求解角度，或者是在已知部分边长和角度的情况下，进一步求解未知的边长。

余弦定理的表达式是这样的：

\[ c^2 = a^2 + b^2 - 2ab\cos C \]

（同样地，也有关于a和b的类似表达式，通过改变边和角的位置即可得到。）

这个公式告诉我们，在三角形中，任意一边的平方等于其他两边的平方和减去这两边与它们夹角的余弦的积的两倍。余弦定理的出现，使得我们在只知道三角形的两边和它们之间的夹角时，也能精确地计算出第三边的长度，或者在已知三边长度时，求出任意一角的余弦值，进而求得角度。

应用场景：余弦定理在工程测量、建筑设计、物理力学等领域都有重要应用。比如，在建筑设计中，工程师需要根据建筑物的尺寸和地基的倾斜度来计算支撑结构的强度，这时余弦定理就能提供关键的数据支持。

两者的联袂演出：解决三角问题的双剑合璧

正弦定理和余弦定理，虽然各有侧重，但在解决复杂的三角形问题时，往往能够联袂演出，形成强大的合力。它们之间并不是孤立存在的，而是相互补充，共同构建了一个完整的三角形知识体系。当你面对一个三角形问题时，可以先观察已知条件，如果涉及到角度与边长之间的直接换算，正弦定理可能是你的首选；而如果你需要利用边长信息来求解角度，或者验证三角形的形状和稳定性，那么余弦定理将是你的得力助手。

结语

总之，正弦定理和余弦定理是数学中不可或缺的工具，它们以简洁而深刻的方式揭示了三角形边长与角度之间的内在联系。无论是探索自然界的奥秘，还是解决日常生活中的实际问题，这两个定理都发挥着不可替代的作用。通过掌握它们，我们不仅能够更加灵活地处理三角形相关的数学问题，还能够培养起严谨的逻辑思维和敏锐的洞察力。正如我们在探索三角形世界的过程中所感受到的那样，数学之美，往往就藏在这些看似简单却蕴含无限智慧的定理之中。