揭秘!一立方计算方法大公开,轻松掌握空间计量的奥秘
在探讨“一立方怎么算”这一基础而重要的数学与物理概念时,我们首先需要明确“立方”这一概念的本质及其在日常生活、工程、科学计算中的广泛应用。立方,简而言之,是三维空间中物体占据的体积度量,其计算基于长、宽、高的乘积,单位通常是立方米(m³)、立方厘米(cm³)等。下面,我们将从几个不同的角度深入浅出地解释如何计算一立方,并辅以实例说明,以帮助读者全面理解。
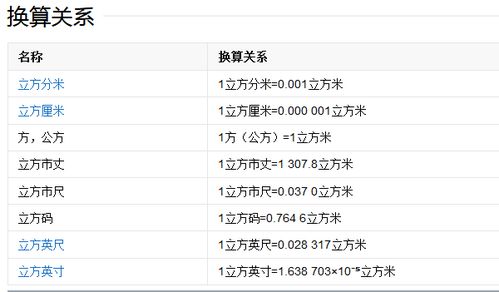
一、立方的基本概念
定义:立方,指的是一个物体在三维空间内占据的体积大小,具体计算方式为将该物体的长度(L)、宽度(W)和高度(H)相乘,即V = L × W × H。这里的V代表体积,是立方的度量结果。
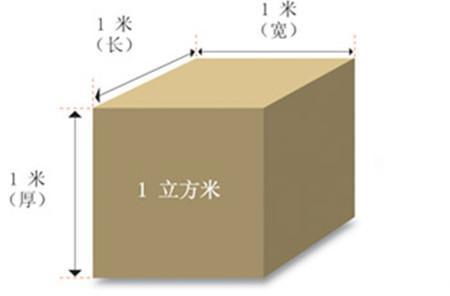
单位:体积的单位可以是立方米、立方分米、立方厘米等,根据测量对象的尺寸和需要选择合适的单位。在国际单位制中,立方米(m³)是最常用的体积单位。
二、如何计算一立方
1. 规则形状物体的立方计算
长方体:对于最常见的长方体,其立方计算最为直接。假设长方体的长为L米,宽为W米,高为H米,则其体积V(立方米)为:
\[ V = L \times W \times H \]
例如,一个房间的长为5米,宽为4米,高为3米,则该房间的体积为:
\[ V = 5 \times 4 \times 3 = 60 \text{立方米} \]
正方体:正方体是特殊的长方体,其长、宽、高均相等,设边长为a米,则体积V为:
\[ V = a^3 \]
若正方体的边长为2米,则体积为:
\[ V = 2^3 = 8 \text{立方米} \]
圆柱体:虽然圆柱体不是严格的长方体或正方体,但其体积也可以通过类似的思路计算。圆柱体的体积V(立方米)为底面积πr²(r为底面半径,π取3.14)乘以高h:
\[ V = \pi r^2 \times h \]
如一个底面半径为1米,高为2米的圆柱体,其体积为:
\[ V = 3.14 \times 1^2 \times 2 = 6.28 \text{立方米} \]
2. 不规则形状物体的立方估算
对于不规则形状的物体,直接计算其精确体积可能较为复杂,通常需要采用估算方法。常见的方法包括:
排水法:将物体完全浸入水中,测量水位上升的体积即为物体的体积。
分割法:将不规则物体近似地分割成多个规则形状的部分,分别计算各部分的体积后求和。
三维扫描与建模:利用现代科技手段,如三维扫描仪对物体进行扫描,然后通过计算机软件构建物体的三维模型,进而计算其体积。
三、立方的应用实例
1. 日常生活
家具选购:在购买家具时,了解家具的体积可以帮助我们判断其是否适合家中的空间。
储物规划:合理规划储物空间,计算所需空间体积,确保物品有序存放。
2. 工程建设
土方工程:在土木工程如道路建设、房屋基础开挖中,需要精确计算所需挖掘或回填的土方体积。
建筑设计:建筑设计时需考虑建筑物的整体体积,以评估其对土地的占用情况及建设成本。
3. 科学研究
物理学:在研究物质的性质时,体积是重要参数之一,如密度计算(质量/体积)。
化学工程:在化工反应釜的设计中,需根据反应物及生成物的体积来确定反应器的容积。
四、结语
通过上述介绍,我们可以清晰地看到,“一立方怎么算”不仅是一个简单的数学问题,更是涉及到我们日常生活的方方面面,从家具摆放到工程建设,再到科学研究,都离不开对体积的准确计算。掌握立方的计算方法,不仅能够帮助我们更好地理解和利用空间,还能在解决实际问题时提供有力的数学支持。希望本文能够帮助读者全面理解“一立方”的计算原理及应用,为日后的学习、工作和生活带来便利。
- 上一篇: 初学者如何学习并实践插花技巧?
- 下一篇: 如何在线完成学历认证流程
新锐游戏抢先玩
游戏攻略帮助你
更多+-
03/03
-
03/03
-
03/03
-
03/03
-
03/03









