揭秘！长方体的体积公式：轻松掌握三维空间的度量艺术

在几何学的广阔领域中，长方体作为一种基础而重要的三维图形，其体积计算不仅是数学教育的基石，也是日常生活与科学探索中不可或缺的工具。长方体的体积公式，简洁而深刻地揭示了空间形状与其容量之间的数学关系，即长度、宽度与高度的乘积。本文将从几个不同维度出发，深入探讨长方体的体积公式，揭示其背后的数学原理、实际应用以及对学生思维能力的培养价值。

一、数学原理的探索

长方体的体积公式，即`V = l × w × h`，其中`V`代表体积，`l`、`w`、`h`分别代表长方体的长度、宽度和高度。这一公式的诞生，源于对空间度量本质的深刻理解。在数学上，体积是对三维空间内物体占据空间的量的度量，而长方体作为由三组平行且等长的线段围成的立体图形，其体积的计算自然而然地关联到了它的三个维度尺寸。

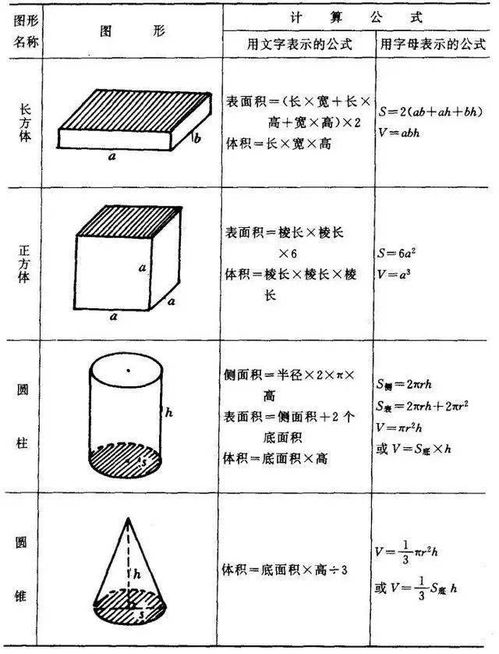
通过积分学的视角，我们可以将长方体的体积视为无数个微小的平行六面体（可视为极薄的长方体）体积之和。当这些微小长方体的厚度趋于无穷小时，它们的体积之和就趋近于整个长方体的体积。而这一过程，实际上是对`l × w`（即底面积）进行高度`h`上的积分，直接得出了`V = l × w × h`的公式。尽管对于初学者而言，积分理论可能略显复杂，但它为我们提供了一个从连续变化角度理解长方体体积公式的深刻视角。

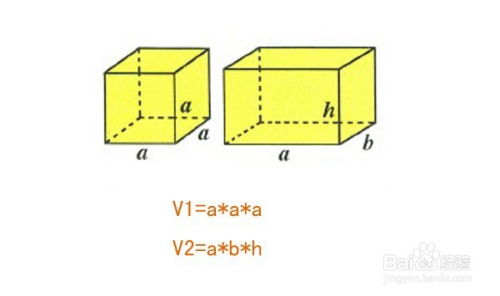
二、实际应用的广泛性

长方体的体积公式，在日常生活中有着极为广泛的应用。从简单的家居设计到复杂的工程计算，几乎无处不见其身影。

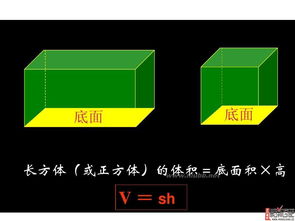
家居设计：在装修房屋时，我们可能需要计算房间能容纳多少家具，这时就会用到长方体的体积公式来估算沙发、床、衣柜等大件物品的占用空间。

物流运输：物流公司需要准确计算货物的体积，以便合理安排运输车辆和存储空间，长方体的体积公式成为不可或缺的工具。

建筑工程：在建筑领域，设计师需要计算墙体、楼板等构件的体积，以确定材料用量和施工成本，长方体的体积计算是基础中的基础。

农业灌溉：在农业领域，计算蓄水池或水塘的蓄水量时，也常常将其视为长方体（或近似长方体）进行体积估算，从而科学安排灌溉计划。

三、教育价值的体现

长方体的体积公式不仅是数学知识的一部分，更是培养学生空间想象力、逻辑推理能力和问题解决能力的重要载体。

空间想象力的培养：通过观察和操作长方体模型，学生可以直观地感受到三维空间的概念，逐步构建起对空间形状、大小及相互关系的认知框架。这种空间想象力是学习数学、物理、工程等多门学科所必需的。

逻辑推理能力的锻炼：在学习和应用长方体体积公式的过程中，学生需要理解公式中各个变量的含义及其相互之间的关系，这要求他们具备较强的逻辑推理能力。通过不断地练习和思考，学生的逻辑思维将得到有效的锻炼和提升。

问题解决能力的培养：面对实际问题时，学生能够运用长方体体积公式进行分析、计算和判断，从而找到解决问题的方法。这种将理论知识应用于实践的能力，是学生未来生活和工作中不可或缺的重要素质。

四、跨学科融合的桥梁

长方体的体积公式还是跨学科知识融合的桥梁。在物理学中，密度、质量与体积的关系（ρ=m/V）揭示了物质的基本属性；在经济学中，成本计算时往往需要考虑到物品的体积因素；在计算机图形学中，三维建模和渲染技术更是离不开对物体体积的精确计算。因此，掌握长方体的体积公式，不仅有助于学生更好地学习数学本身，还能为他们未来学习其他学科打下坚实的基础。

结语

综上所述，长方体的体积公式作为几何学中的一个基本而重要的概念，其背后蕴含着丰富的数学原理、广泛的应用价值以及深刻的教育意义。通过多维度地学习和理解这一公式，我们不仅能够掌握计算长方体体积的方法，更能在这一过程中培养空间想象力、逻辑推理能力和问题解决能力，为未来的学习和生活奠定坚实的基础。