如何计算空间内一点到直线的距离？求解公式是什么？

在探讨数学领域中关于“空间中的点到直线的距离公式”这一深刻而又基础的问题时，我们首先需要理解其背后的几何与代数意义。空间，作为三维世界的抽象表达，其中的点、线、面等元素构成了复杂而有序的几何结构。而点到直线的距离，则是这一结构中最基本也是最具实用价值的度量方式之一，广泛应用于工程学、物理学、计算机科学等多个领域。

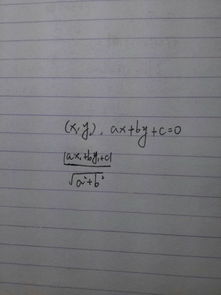
空间中的点与直线

在三维空间中，点是最基本的几何元素，可以用三个坐标值（如x, y, z）来精确定位。直线则是由无数个点组成，且满足某一特定线性方程（如Ax + By + Cz + D = 0）的集合。当我们谈论“点到直线的距离”时，实质上是在求解一个特定点到这条直线上所有点之间距离的最小值。

距离公式的推导

为了找到这个最小值，我们可以利用向量方法来进行推导。首先，假设我们有一个点P(x0, y0, z0)，以及一条由线性方程Ax + By + Cz + D = 0定义的直线L。直线L的方向向量可以由系数A、B、C构成，即向量v = (A, B, C)。

1. 构造直线的参数方程：为了方便计算，我们可以将直线L表示为参数方程形式。设直线L上任意一点为Q(x, y, z)，则Q点满足：

\[

\begin{cases}

x = x_1 + at \\

y = y_1 + bt \\

z = z_1 + ct

\end{cases}

\]

其中，(x1, y1, z1)是直线L上已知的一点（通常通过解方程组得到），a、b、c是方向向量v的单位化向量分量（即a=A/√(A²+B²+C²), b=B/√(A²+B²+C²), c=C/√(A²+B²+C²)），t为参数。

2. 计算向量PQ：向量PQ从点P指向直线L上的点Q，其坐标为：

\[

\overrightarrow{PQ} = (x - x_0, y - y_0, z - z_0)

\]

将Q点的参数方程代入，得到向量PQ关于t的表达式。

3. 利用向量点积求垂直距离：由于点到直线的最短距离是垂直于直线的，因此PQ与方向向量v的点积应为0（即PQ⊥v）。通过这一性质，我们可以解出参数t的值，进而找到使PQ最短的Q点坐标。

4. 计算距离：最后，使用距离公式计算P点到找到的最短距离点Q之间的距离，即得到了点P到直线L的距离d：

\[

d = \sqrt{(x_Q - x_0)^2 + (y_Q - y_0)^2 + (z_Q - z_0)^2}

\]

其中，(xQ, yQ, zQ)是使PQ最短的Q点坐标。

简化公式

上述过程虽然直观，但在实际应用中，我们更倾向于使用简化后的公式直接计算。对于点P(x0, y0, z0)到直线Ax + By + Cz + D = 0的距离d，其简化公式为：

\[

d = \frac{|Ax_0 + By_0 + Cz_0 + D|}{\sqrt{A^2 + B^2 + C^2}}

\]

这个公式直接利用了点到直线的垂直距离性质，避免了求解直线参数方程和寻找最短距离点的复杂过程，极大地简化了计算。

应用场景

空间中的点到直线距离公式在多个领域都有着广泛的应用。例如，在机器人导航中，机器人需要计算自身到目标路径（可视为直线）的最短距离以确定最优行进方向；在CAD/CAM（计算机辅助设计与制造）中，设计师需要精确测量零件上某点到设计基准线（直线）的偏差；在三维建模和渲染中，计算物体表面点到光源直线路径的距离对于实现真实感渲染至关重要。

结语

综上所述，空间中的点到直线距离公式是数学几何学中一个既基础又重要的概念，它不仅深化了我们对三维空间结构的理解，更为众多实际应用提供了有力的数学支撑。通过掌握这一公式，我们能够更加精准地描述和分析空间中的位置关系，推动科学技术的不断进步。