揭秘！点到直线距离公式的神奇推导过程，你了解吗？

在数学的广阔天地里，点到直线距离的公式是一个既基础又重要的概念，它不仅在日常解题中频繁出现，还深刻影响着我们对空间关系的理解。想象一下，你站在一条笔直的公路旁，想要知道自己离这条路的距离有多远，这时候，点到直线距离的公式就派上了大用场。那么，这个公式是如何推导出来的呢？让我们一起揭开它的神秘面纱。

点到直线距离公式的定义

首先，我们需要明确一个定义：从直线外一点到这条直线的垂线段长度，就叫做点到直线的距离。这里的“垂线段”是关键，因为它保证了从点到直线的所有连线中，这条线是最短的。

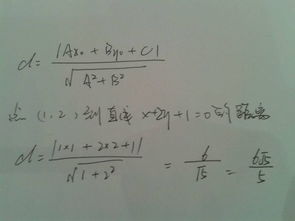
推导过程简述

点到直线距离的推导过程，实质上是一个结合了几何与代数方法的巧妙构造。我们假设直线方程为 `Ax + By + C = 0`，而直线外的一个点为 `P(x0, y0)`。我们的目标是找到点P到这条直线的最短距离，即垂线段PQ的长度。

第一步：求垂线方程

为了找到点P到直线的垂线，我们需要知道这条垂线的斜率。由于直线与垂线垂直，它们的斜率之积为-1。设直线 `Ax + By + C = 0` 的斜率为 `-A/B`（注意，这里B不能为0，否则直线垂直于x轴，情况会稍有不同），则垂线的斜率为 `B/A`。因此，过点P的垂线方程可以表示为 `y - y0 = (B/A)(x - x0)`。

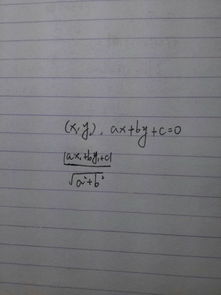
第二步：求交点坐标

接下来，我们需要找到直线与垂线的交点Q。这可以通过联立两个方程来实现：

直线方程：`Ax + By + C = 0`

垂线方程：`y - y0 = (B/A)(x - x0)`

将垂线方程变形为 `y = (B/A)x + y0 - (B/A)x0`，然后代入直线方程，解出x和y的值，即可得到交点Q的坐标。这个步骤可能涉及一些代数运算，但本质上是解一个二元一次方程组。

第三步：计算距离

得到交点Q的坐标后，我们就可以利用两点间距离公式来计算PQ的长度了。两点间距离公式为：

\[

d = \sqrt{(x2 - x1)^2 + (y2 - y1)^2}

\]

将点P和点Q的坐标代入公式，即可得到点到直线的距离。

具体公式推导

为了更直观地展示推导过程，我们可以将上述步骤中的计算具体化。假设交点Q的坐标为 `((B^2x0 - ABy0 - AC)/(A^2 + B^2), (A^2y0 - ABx0 - BC)/(A^2 + B^2))`（这个坐标是通过联立方程求解得到的，具体过程可能因篇幅限制而省略）。

代入两点间距离公式，我们有：

\[

PQ = \sqrt{\left(\frac{B^2x0 - ABy0 - AC}{A^2 + B^2} - x0\right)^2 + \left(\frac{A^2y0 - ABx0 - BC}{A^2 + B^2} - y0\right)^2}

\]

经过一系列代数运算（包括平方、合并同类项等），最终可以化简为：

\[

PQ = \frac{|Ax0 + By0 + C|}{\sqrt{A^2 + B^2}}

\]

这就是点到直线距离的公式。它告诉我们，只要知道直线的方程和一个点的坐标，就可以轻松地计算出这个点到直线的距离。

结语

通过上述推导，我们不难发现，点到直线距离的公式背后蕴含着丰富的几何与代数知识。它不仅是一个简单的公式，更是我们理解空间关系、解决实际问题的重要工具。希望这篇文章能够帮助你更好地理解点到直线距离的推导过程，感受数学的魅力与乐趣。在未来的学习和生活中，不妨多运用这个公式，让数学成为你探索世界的得力助手。