揭秘!正方体面积计算的神秘公式,你真的了解吗?
在探讨几何学的广阔领域中,正方体作为一种基础而重要的三维立体图形,其面积与体积的计算是几何学教育不可或缺的一部分。尽管“正方体”这一术语直接关联于三维空间中的物体,当我们提及“正方体的面积”时,实际上是在讨论其各个表面的总面积,因为正方体有六个完全相同的正方形面。下面,我们将从多个维度深入解析正方体的面积公式,以及这一公式背后的几何原理和应用。
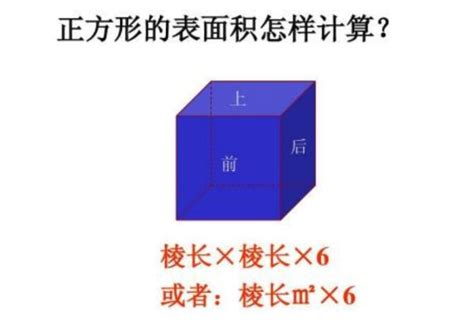
一、正方体的基本属性
首先,了解正方体的基本属性是掌握其面积公式的前提。正方体,也称为立方体,是所有棱长都相等的特殊六面体。它的每一个面都是一个正方形,具有四条等长的边和四个直角。正方体的空间对称性极高,不仅面与面之间对称,而且棱与棱、顶点与顶点之间也呈现出完美的对称性。这种高度的对称性使得正方体在日常生活、建筑设计、工程学以及数学研究中都有着广泛的应用。
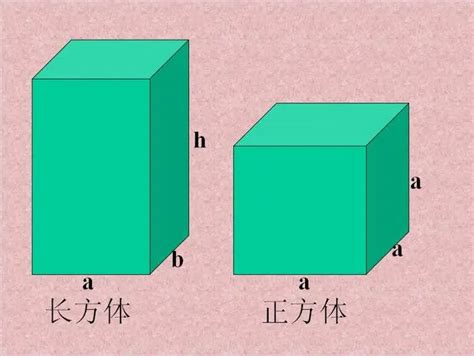
二、正方体的面积计算
1. 单个面的面积
由于正方体的每一个面都是正方形,计算单个面的面积就转化为了计算正方形的面积。正方形的面积公式为:边长(a)的平方,即S_正方形 = a^2。因此,对于正方体而言,任意一个面的面积都是其棱长(假设为a)的平方。
2. 总面积的计算
正方体有六个完全相同的面,所以其总面积(也称为表面积)就是单个面面积的六倍。即:S_总 = 6 × S_正方形 = 6 × a^2。这个公式简洁而直接地给出了正方体表面积的计算方法,是几何学中的基础公式之一。
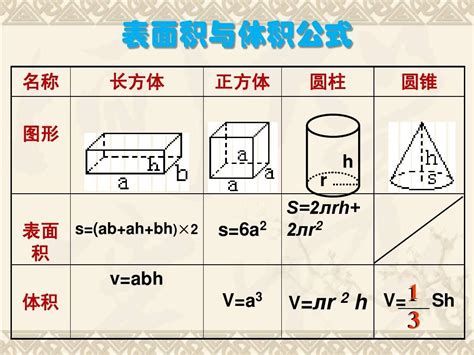
三、面积公式的几何解释
从几何学的角度来看,正方体面积公式的推导过程充满了直观与逻辑的美感。想象一个正方体模型,你可以清晰地看到它由六个正方形面围合而成。当你想要计算这个物体的“外部覆盖面积”时,实际上就是将这些面的面积加起来。由于所有面都是相同的,所以问题简化为计算一个面的面积,然后乘以6。这种几何直观性不仅帮助我们记忆公式,还加深了我们对三维空间形状的理解。

四、面积公式的应用
1. 日常生活中的应用
正方体的面积公式在日常生活中有着广泛的应用。比如,在计算纸箱、礼品盒等包装材料的用量时,就需要知道其表面积。又如,在家庭装修中,如果需要为房间内的某个立方体物品(如书架、衣柜)喷涂油漆或贴纸,也需要先计算出其表面积来确定所需材料的数量。
2. 物理学与工程学中的应用
在物理学和工程学中,正方体面积的计算也具有重要意义。例如,在计算物体表面受到的压力或热量传递时,表面积是一个关键参数。对于立方体形状的设备或部件,通过正方体面积公式可以快速准确地得出其表面积,进而进行后续的力学分析或热学计算。
3. 数学教育中的价值
在数学教育中,正方体面积的计算不仅是学习几何知识的基础,也是培养学生空间想象能力和逻辑推理能力的重要手段。通过动手制作正方体模型、观察其结构特点、推导面积公式等活动,学生可以更加直观地理解三维空间中的几何概念,为后续更复杂的几何学习打下坚实的基础。
五、结论
综上所述,正方体的面积公式(S_总 = 6 × a^2)是几何学中的一个基本而重要的公式。它不仅具有简洁明了的形式,而且蕴含着丰富的几何意义和广泛的应用价值。通过对这一公式的深入学习和理解,我们可以更好地掌握三维空间中的几何知识,提高解决实际问题的能力。同时,正方体的面积计算也是培养空间想象能力和逻辑推理能力的重要途径,对于促进学生的全面发展具有重要意义。
- 上一篇: 这个LOGO代表什么意思?
- 下一篇: 尊享席位,自助式冷餐盛宴服务流程全揭秘
新锐游戏抢先玩
游戏攻略帮助你
更多+-
03/07
-
03/07
-
03/07
-
03/07
-
03/07










