如何计算正方形的表面积？公式是什么？

在探讨“正方形表面积公式怎么做”这一主题时，首先需要澄清一个常见的误区：正方形，作为一个二维平面图形，并不具备“表面积”这一概念。表面积是三维立体图形（如正方体、长方体、球体等）所有外部面的面积之和。正方形，仅由四条等长的边和四个相等的角（每个角均为90度）围成的平面图形，仅有一个面，即它的面积，而非表面积。

然而，鉴于您希望以此为主题展开一篇文章，并希望读者能够全面理解与此相关的知识点，我们可以将话题稍作延展，从正方形的基本属性讲起，进而介绍到与其相关的三维图形——正方体的表面积计算，以此作为回应。

探索正方形与正方体的世界：从面积到表面积

在数学的浩瀚宇宙中，几何图形以其独特的形态和性质吸引着无数求知者的目光。正方形，作为最基本也最常见的二维图形之一，其简洁与对称之美令人赞叹。而当我们跨越维度，步入三维空间，正方体（也称为立方体）则以其稳固的结构和丰富的几何特性成为我们探索的新对象。今天，我们就一同走进这个由正方形构成的立体世界，从正方形的面积计算开始，逐步理解正方体的表面积公式。

一、正方形的基础认知

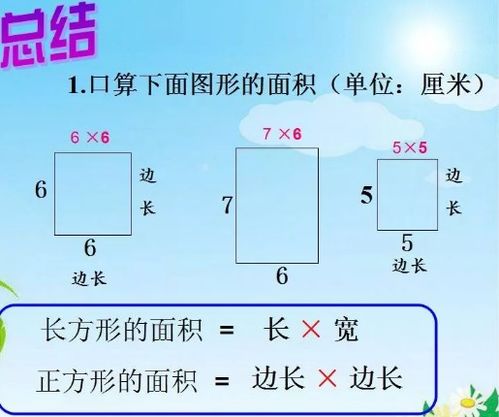
正方形，一个四边等长、四角皆为直角的四边形，其面积计算是几何学中最基础的知识点之一。正方形的面积计算公式为：面积 = 边长 × 边长，或简写为S = a²，其中a为正方形的边长。这个公式简单直观，是理解后续复杂几何问题的基石。

二、从正方形到正方体：维度的跨越

当我们把正方形的概念拓展到三维空间，便得到了正方体。正方体是由六个完全相同的正方形面围成的立体图形，每个面都垂直于其他四个面且平行于另外两个面。这种结构不仅美观，还赋予了正方体许多独特的性质，其中之一就是其表面积的计算。

三、正方体的表面积计算

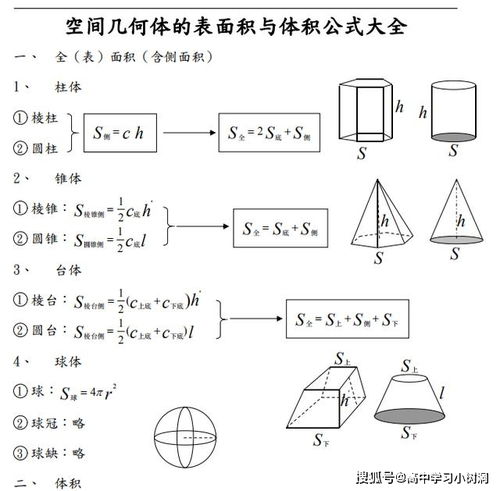
正方体的表面积，即其所有外部面的面积之和。由于正方体有六个面，且每个面都是完全相同的正方形，因此计算其表面积就变得相对简单。具体步骤如下：

1. 确定一个面的面积：首先，我们需要知道正方体一个面的面积。由于正方体的每个面都是正方形，所以我们可以直接使用正方形的面积公式S = a²来计算，其中a为正方体的棱长（也即正方体的一个边的长度，与正方形边长同义）。

2. 计算所有面的面积之和：既然正方体有六个面，且每个面的面积都相同，那么正方体的表面积就是六个这样的面的面积之和。因此，正方体的表面积公式为：表面积 = 6 × 一个面的面积 = 6 × a²。

四、表面积公式的应用与意义

正方体的表面积公式不仅是一个数学工具，它在实际生活中也有着广泛的应用。比如，在建筑设计中，设计师需要考虑建筑物的外墙面积以计算所需材料；在包装设计中，了解产品的表面积有助于精确计算包装纸或包装盒的尺寸；在农业生产中，计算农作物的覆盖面积对于施肥、灌溉等管理活动至关重要。而正方体的表面积公式，正是这些实际应用背后的理论基础之一。

五、结语

通过对正方形面积和正方体表面积的探讨，我们不仅回顾了基础的几何知识，还领略了从二维到三维的维度跨越所带来的奇妙变化。正方形的面积计算为我们打开了几何世界的大门，而正方体的表面积公式则让我们在这个世界中走得更远、看得更深。希望这篇文章能够激发您对几何学的兴趣，让您在探索的道路上越走越宽广。

记住，每一个看似简单的公式背后，都蕴含着丰富的数学思想和深刻的自然法则。让我们保持好奇心，继续在数学的海洋中遨游吧！