揭秘!方差计算公式的奥秘,让数据波动一目了然
在探讨数据的波动性与稳定性时,方差(Variance)作为一个核心统计量,扮演着举足轻重的角色。它不仅在学术研究中频繁出现,如经济学、心理学、物理学等多个领域,也是日常生活和工作中分析数据差异性的有力工具。那么,方差的计算公式究竟是什么?它又是如何揭示数据背后隐藏的信息呢?
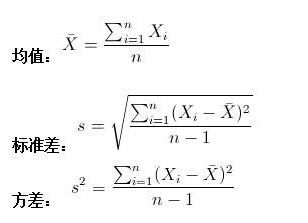
方差的定义与直观理解
首先,让我们从定义出发。方差是衡量数据集中各个数值与其平均数(均值)之间差异的平方的平均数。简单来说,方差越小,表示数据点越趋近于均值,即数据越集中;方差越大,则数据点分布越离散,即数据差异性大。这种度量方式,为我们提供了一个量化数据离散程度的工具。

方差的计算公式
方差的计算公式相对直观,但包含了几个关键步骤,确保了计算的准确性和科学性。对于一个包含n个数值的数据集{x₁, x₂, ..., xₙ},其方差的计算公式如下:

\[
\text{方差} = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2
\]
其中,$\bar{x}$ 是数据集的平均数,计算公式为:
\[
\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i
\]
步骤解析:
1. 计算平均数:首先,我们需要求出数据集中所有数值的算术平均数,即所有数值之和除以数值的数量。
2. 求每个数据点与平均数的差:然后,对于数据集中的每一个数值,计算它与平均数的差。这个差值代表了该数据点偏离中心(即平均数)的程度。
3. 求差的平方:由于我们关心的是偏差的大小,而不关心偏差的方向(即无论是正偏差还是负偏差,我们都认为是对稳定性的一种破坏),因此需要将每个差值取平方。这样,所有的偏差都被转换为了正数,便于后续计算。
4. 求平方差的平均数:最后,将上述所有平方差相加,并除以数值的数量n,得到的就是方差。这个步骤确保了即使数据集很大,方差也能保持在一个相对稳定的范围内,反映了数据整体的离散程度。
方差的应用与意义
方差的应用极为广泛,它不仅是统计分析中的基础工具,还在许多领域发挥着重要作用:
金融分析:在金融市场,方差被用来评估投资组合的风险。高方差通常意味着投资组合的波动性大,即风险较高;而低方差则代表相对稳定的回报。
质量控制:在制造业中,方差用于监控生产过程中的变异性。如果产品质量的方差增大,可能意味着生产流程出现了问题,需要及时调整。
社会科学研究:在心理学、教育学等领域,方差分析(ANOVA)是一种常见的统计方法,用于比较不同组别之间的差异是否显著,从而帮助研究者理解变量之间的关系。
预测模型评估:在机器学习领域,方差也是评估模型泛化能力的一个重要指标。低方差模型往往能够更稳定地适应新数据,减少过拟合的风险。
结语
通过上述介绍,我们可以清晰地看到,方差作为衡量数据离散程度的重要统计量,其计算公式不仅简洁明了,而且蕴含着深刻的数学思想和统计原理。无论是对于学术研究者,还是普通的数据分析爱好者,掌握方差的计算方法,都是深入理解数据、洞察数据背后规律的关键一步。希望这篇文章能够帮助到每一位对“方差的计算公式是什么”感兴趣的朋友,让你在数据分析的道路上更加得心应手。
- 上一篇: 揭秘陶瓷艺术:从泥土到瑰宝的全流程制作工艺
- 下一篇: 高效指南:如何有效投诉中通快递服务问题
新锐游戏抢先玩
游戏攻略帮助你
更多+-
03/04
-
03/04
-
03/04
-
03/04
-
03/04









