揭秘！数学中的三角形余弦定理究竟是什么？

数学三角形余弦定理探析

在数学的广阔天地中，三角形作为最基本的几何图形之一，承载着丰富的数学原理与定理。其中，余弦定理作为揭示三角形边角关系的重要工具，不仅是平面几何的基石，也在立体几何、数形结合等多个领域发挥着重要作用。本文旨在全面解析数学中的三角形余弦定理，带领读者深入理解其概念、推导过程、应用领域及实际意义。

一、余弦定理的基本概念

余弦定理是描述三角形中三边长度与一个角的余弦值之间关系的数学定理。具体来说，对于任意三角形ABC，其中a、b、c分别为三角形的三边长，A、B、C为对应的三个角，余弦定理可以表达为：在三角形ABC中，任意一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。即：

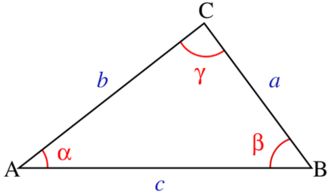
\[ a^2 = b^2 + c^2 - 2bc\cos A \]

\[ b^2 = a^2 + c^2 - 2ac\cos B \]

\[ c^2 = a^2 + b^2 - 2ab\cos C \]

这些公式直观地展示了三角形三边与内角之间的数学联系，是勾股定理在一般三角形情形下的推广。当角C为90°时，余弦定理即退化为勾股定理，因此勾股定理可以视为余弦定理的一个特例。

二、余弦定理的推导

余弦定理的推导方法多种多样，既有基于平面几何的直观证明，也有利用向量、三角函数等现代数学工具的抽象证明。以下简述几种常见的推导方法：

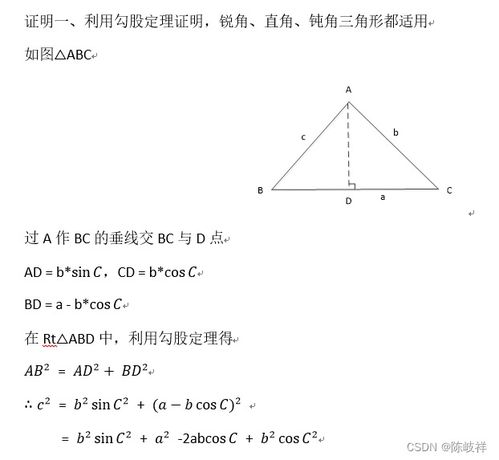
1. 平面几何证法：通过在三角形中作高，利用勾股定理和相似三角形的性质进行推导。这种方法直观易懂，适合初学者理解余弦定理的几何意义。

2. 向量证法：利用向量的数量积公式和三角形法则，将三角形的边表示为向量，并通过向量的数量积推导出余弦定理。这种方法体现了数学中代数与几何的统一，展示了现代数学的简洁与优美。

3. 三角函数证法：利用正弦定理和三角函数的性质，通过变形和推导得到余弦定理的表达式。这种方法需要一定的三角函数基础，但能够更深入地理解余弦定理与三角函数之间的联系。

三、余弦定理的应用

余弦定理在解决三角形相关问题中具有广泛的应用价值，主要体现在以下几个方面：

1. 解三角形：已知三角形的两边及夹角，可以利用余弦定理求出第三边的长度；已知三角形的三边，可以利用余弦定理求出各角的余弦值，进而求出各角的度数。这是余弦定理最直接的应用。

2. 判定三角形的形状：根据余弦定理的推论，若a²+b²=c²，则C为直角；若a²+b²>c²，则C为锐角；若a²+b²

3. 实际问题的解决：余弦定理在工程技术、物理计算等领域有着广泛的应用。例如，在测量无法直接到达的两点间的距离时，可以通过测量其他相关距离和角度，利用余弦定理计算出所需距离；在解决力学问题时，也可以利用余弦定理求解物体的受力情况等。

4. 计算机科学中的应用：在计算机科学领域，余弦定理是智能推荐系统、新闻分类等算法中的基础工具之一。通过对文本、用户行为等数据的向量化处理，计算不同数据之间的余弦相似度，从而实现精准的推荐和分类。

四、余弦定理的实际意义

余弦定理不仅是一个重要的数学定理，更是一个连接理论与实践的桥梁。它揭示了三角形三边与内角之间的深刻联系，为我们理解和解决实际问题提供了有力支持。通过学习和掌握余弦定理，我们可以更加灵活地运用数学知识解决生活中的各种问题，提高我们的逻辑思维能力和创新能力。

同时，余弦定理的广泛应用也体现了数学与其他学科的紧密联系。无论是自然科学、工程技术还是社会科学领域，数学都扮演着不可或缺的角色。余弦定理作为数学中的一个重要定理，其影响力和价值远远超出了数学学科本身，成为推动人类文明进步的重要力量之一。

五、结语

综上所述，三角形余弦定理是数学中一个非常重要的定理。它不仅揭示了三角形三边与内角之间的数学关系，也为解决三角形相关问题和实际问题提供了有力支持。通过学习和掌握余弦定理，我们可以更加深入地理解数学的魅力和力量，为未来的学习和生活奠定坚实的数学基础。希望本文能够帮助读者全面了解三角形余弦定理的概念、推导过程、应用领域及实际意义，激发对数学的兴趣和热爱。